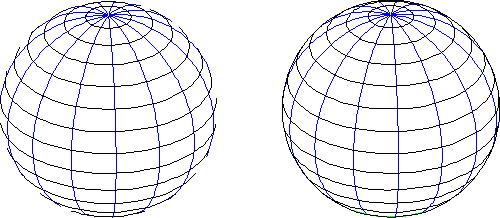
We already pointed out that the use of line graphics results in a contour problem. Roughly speaking the contour of a surface separates its visible points from its invisible points. The representation of a surface without its contour line appears to be unfinished.

Figure 5. A sphere without contour and with contour
We say that a point P on a surface S with a parametric representation (1) is a contour point if and only if
|
n · PC = 0 where n = ¶x/¶u1 × ¶x/¶u2. |
the contour line or contour, for short, of a surface is the set of all its contour points. This is a slightly coarse definition, but serves its purpose well, since it only misses rare cases which are much more easily handled by a slight change in the perspective than by a more precise definition which would involve a very time consuming additional check. Putting
xjk = ¶xk/¶uj (k = 1,2,3; j = 1,2)
and PC = (v1,v2,v3), we obtain from (2)|
v1(u1,u2) |
x11(u1,u2) |
x21(u1,u2) |
||
|
f(u1,u2) = det |
v2(u1,u2) |
x12(u1,u2) |
x22(u1,u2) |
= 0 |
|
v3(u1,u2) |
x13(u1,u2) |
x23(u1,u2) |
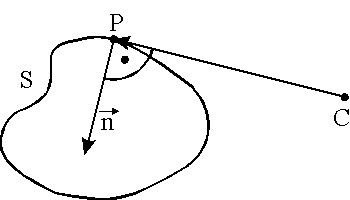
Figure 6. The concept of a contour point
The determination of the contour line of a surface in the general case involves a numerical method to find the zeros of a real-valued function of two real variables in a domain. An algorithm and its implementation can be found in [2].
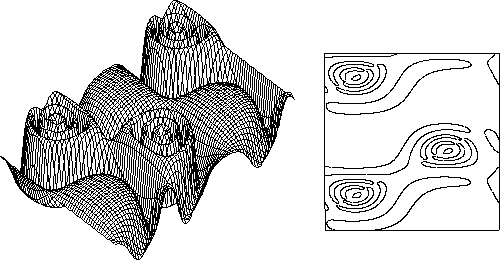
Figure 7. An explicit surface and the projection of its contour line in the parameter plane
The same algorithm can be used to find the line of intersection of a surface with a plane. Let S be a surface with a parametric representation (1) and E a plane through a point P and orthogonal to the vector n=(n1,n2,n3), that is E is given by the equation
|
(OX - OP) · n = 0. |
We put a0 = OP · n and obtain the intersection of S and E from
f(u1,u2) = x(u1,u2) · n - a0 = åk3= 1 nkxk(u1,u2) - a0 = 0.
Example 3.
(a) The contour of surfaces of revolution
(b) Lines of intersection of planes and surfaces of revolution
(c) Lines of intersection of surfaces of revolution
The contour problem and the problem to find lines of intersection of surfaces and planes has been solved in the general case.
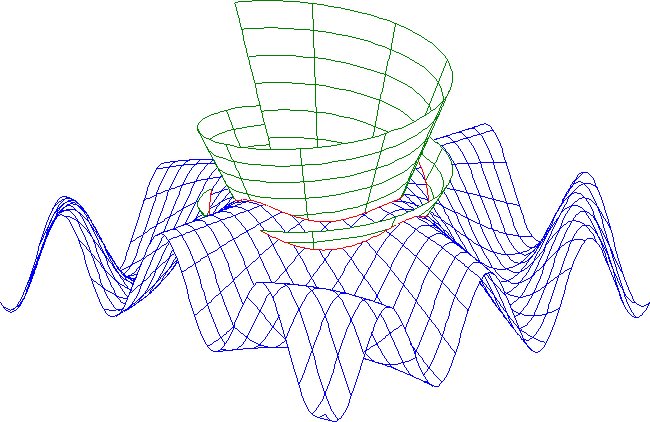
Figure 8. The intersection of an explicit surface and an exponential cone
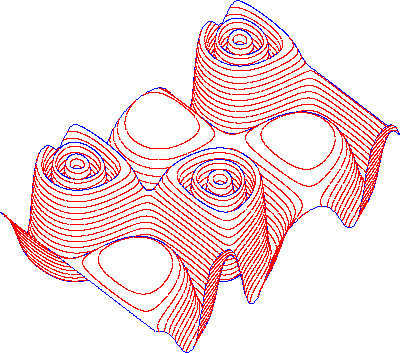
Figure 9. Level lines on an explicit surface