The visibility of points of a surface S is tested by the procedure check. There are two methods in Check, namely S.Visibility(P;Vis), which checks whether a point P on S is invisible with respect to S in which case Vis = FALSE, and S.NotHidden(Q;NotHid), which checks if an arbitrary point Q in space is hidden by S in which case NotHid = FALSE. The method S.NotHidden is very useful in the simultaneous representation of more surfaces than one.
A point P of a given surface S in a class S of surfaces is visible, that is
Check = TRUE
if and only if
Vis = TRUE in S.Visibility(P;Vis)
and
Not.Hid = TRUE in S*.NotHidden(P;NotHid)
for all S* Î S\{S}
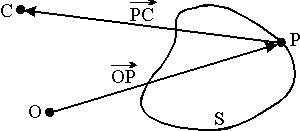
Let S be a surface with parametric representation
|
x(ui) = (x1(u1,u2),x2(u1,u2),x3(u1,u2)) ((u1,u2) Î D) |
where D Ì R2 is a domain, P Î S be a point with position vector OP and C be the centre of projection. Then Vis = FALSE if and only if
x(ui) = OP + t PC for some (u1,u2) Î D and t > 0.

Figure 4. The natural value for Vis
Example 2. The visibility of surfaces of revolution
The visibility problem has been solved for explicit, ruled, potential, tubular and general screw surfaces, for exponential cones and surfaces of revolution.