2. 2. The perspective of the background
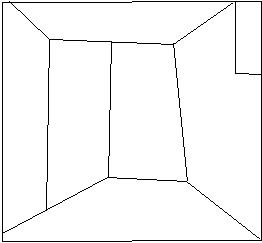
Consider now the room posed as a background of the painting. Its essential linear layout is displayed in Sketch 8. Immediately we realise something wrong is there.
Sketch 8
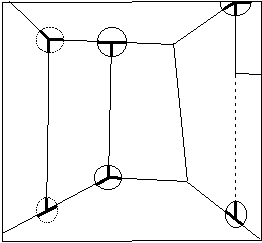
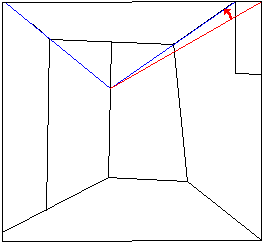
In fact we face an impossible 3D object, where the sides connecting the walls to each other have ambiguous or even mutually inconsistent extremities; it is displayed in Sketch 9, which shows three edges (one of them being an implicit, dashed line) whose opposed extremities are highlighted by means of circles: one end of these sides has a trihedral junction, where three distinct edges meet, while at the opposite extremity, two out the three edges are aligned, giving rise to a dihedral T-junction. The same pattern is repeated three times, swapping up and down dihedral and trihedral junctions. Once again we guess something iterative in the composition.
Sketch 9

Now look at Sketch 10, which shows a rotatory pathway along the edges, like in a spiral. Indeed, the spiral is a recurrent motif in Klee; it is seen as both a peculiar natural form and a metaphysical sign; really Klee attached to the spiral very special meanings, in terms of growth or death, according to the different possible verses (centrifugal or centripetal) one goes along it
[16]; the spiral motif as a symbol of organic growth connects once again Klee to DíArcy Thompson [17].Sketch 10
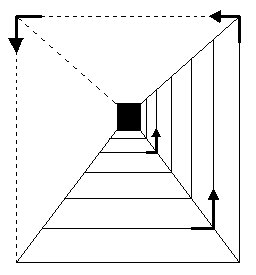
Looking at Chess one has the sensation that the spiral motion is somehow connected with the perspective structure of the room. In fact, observing Kleeís pedagogical sketches on the perspective, often we meet suggestions of spirals around the vanishing points
[18], as in a cob-web, similar to that in Sketch 11. In other words, it seems that Klee conceived the vanishing point as a sort of attractor, even though the conventional rules of perspective doesnít permit that.Sketch 11
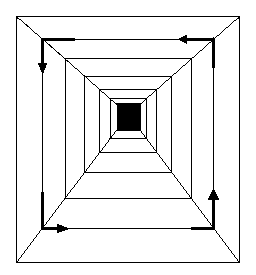
Indeed (see Sketch 12) following the pathway described by the perspective lines, we realise that there canít be a true spiral, but instead a close, rectangular circuit, which perhaps explains why Klee in the most cases didnít complete his perspective rotatory schemes.
Sketch 12
Kleeís writings about perspective dates back to the middle of the 20ís, during his early pedagogical activity at Bauhaus. A few years later Klee seems to discover something interesting about the vanishing point as attractor of an iterative process. In fact, once the vanishing point is chosen, a possible start for the planar perspective construction is to join it (at least ideally) with the four vertex of the rectangle that frames the depicted scene with four diagonal lines, as shown in Sketches 11 and 12. In so doing, vertical and horizontal lines generate rectangles (Sketch 12) whose vertex lay on the diagonals, and they form those close pathways we already discussed.
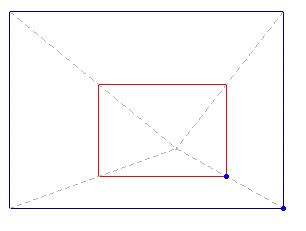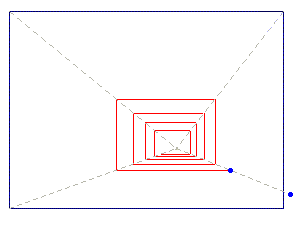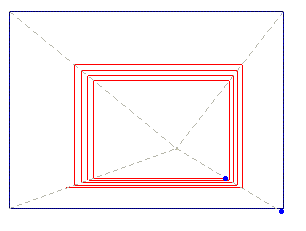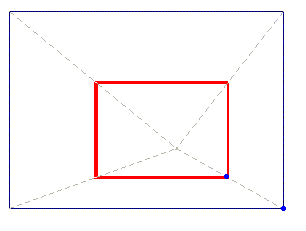
But see now Animation 7, which displays Kleeís discover: declining one of the diagonals from the vertex of the starting rectangle, the perspective spiral he was interested in, made with horizontal and vertical lines, can be obtained: in so doing the spiral can converge to the vanishing point, or diverge to the infinity.
Animation 7
Thus Klee speculated on a new kind of perspective, that generalises the conventional one; indeed, Animation 7 shows that the conventional perspective rules can be seen as a particular, intermediate case of the new ones (convergence or divergence), because the iterations also can produce the closed rectangular pathways of the conventional perspective (a periodic solution). In short, the system can: converge to a point (vanishing point) or converge to a cycle (conventional perspective) or finally diverge to the infinity.
How does it apply to the painting we are discussing?
Let us observe Sketch 13: the upper-right main diagonal of the perspective slightly declines from the upper-right corner of the painting, which may be a possible reason for the insertion of the little windows in that corner.
Sketch 13
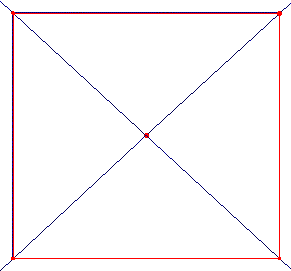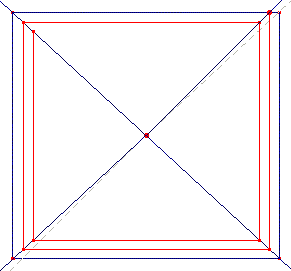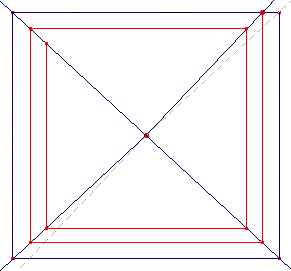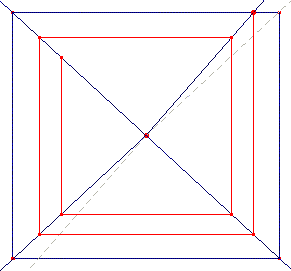
Animation 8 help us understand some temporary consequences of that slight declining of the diagonal line in the perspective construction of the painting.
Animation 8
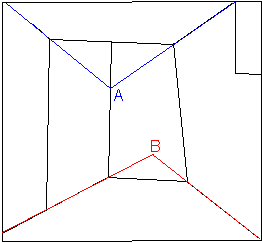
So far we speculated on a possible new perspective construction, starting from the suggestion of a spiral motion of the room sides in the painting Chess. But the same picture contains a second important clue about a generalised perspective construction. Let us observe the four main diagonals of the painting, displayed in Sketch 14. They clearly suggest the presence of two distinct vanishing points, namely A and B.
Sketch 14
We know that Klee theorised the so-called stray centres (or stray viewpoints)
[19], which introduces the simultaneous presence of multiple but moving viewpoints inside the composition. Regardless of the way one accomplishes it in the different cases, the idea of enlarging the perspective by multiplying the viewpoints (and consequently the vanishing points) in the same representation is shared by a number of different artists and artistic currents in the first half of the 900ís, along with the use of non-Euclidean geometry concepts and the ubiquitous suggestions of the fourth dimension [20]. In the early 20ís, Klee himself introduced different viewpoints in the composition, with a number of different solutions. But the one adopted in the early 30ís in Chess is absolutely original: indeed the doubling of the vanishing point is grafted on the idea of iterative construction of the perspective we presented above, and gives rise to unexpected outcomes.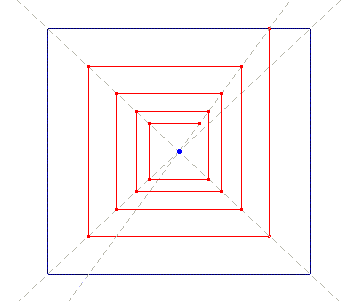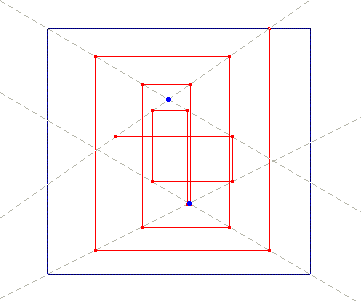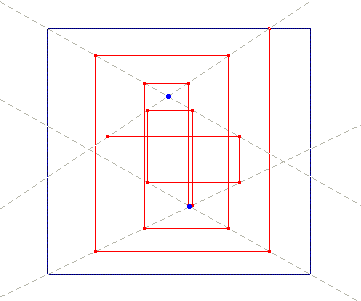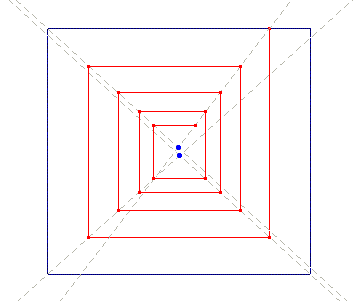
What happens, if we double the vanishing point inside our iterative construction? The situation is depicted by means of Animation 9, which displays the intricate dynamics of the iterative system, caused by the doubling of the vanishing point; indeed it seems to introduce an element of unpredictability: we really face with something chaotic.
Animation 9

Animation 10 applies to Chess the technique presented in Animation 9, in order to further explain its genesis. As a consequence of the doubling of the vanishing point, the system starts to behave irregularly, and the trajectory followed by iterations is no more spiralling, but an unpredictable, irregular, chaotic pathway.
Animation 10
Now a further interesting observation: Klee preferred to stop the iterations just at the edge of the irregularity, to maintain the spiral motion he was interested in: see Animation 10, where indeed I removed the last three segments of the polygonal, just because (as we shall see better later) they have no correspondent in the actual painting.
The choice to push systems to irregular behaviours, and to stop pushing it just at the edge of chaos is quite typical of Klee. Another remarkable example is The truth about the palm-leaf, already cited above.
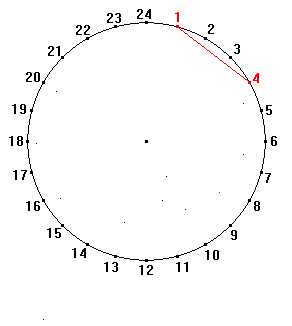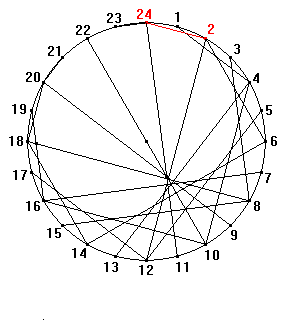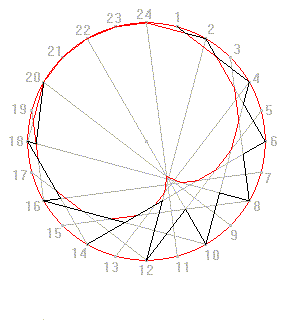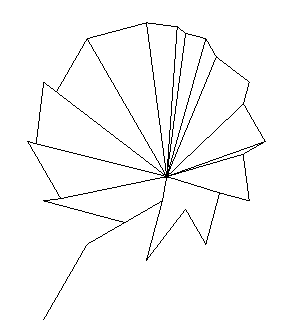
Indeed, if we look once again at Animation 6, we can see that two distinct iterative procedures are applied consecutively: the one of the cords inside the circle, which envelopes the cardioids, and the second one, which zigzagging through those cords generates the outline of the leaf. Notice that the outline is highly irregular, and this effect is openly wanted by Klee. However Klee rearranged the composition only by shifting its barycentre from the centre of the circle to the singularity of the cardioids, staring from there the radiuses which restore equilibrium and harmony inside the drawing.
Animation 6