2. 1. The perspective of the coloured bars
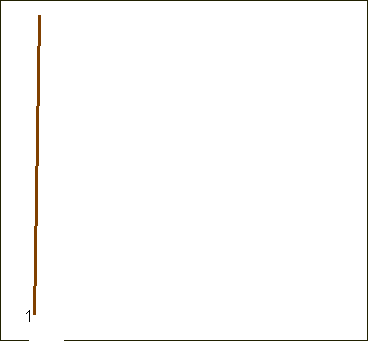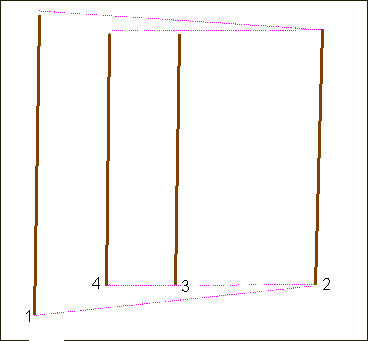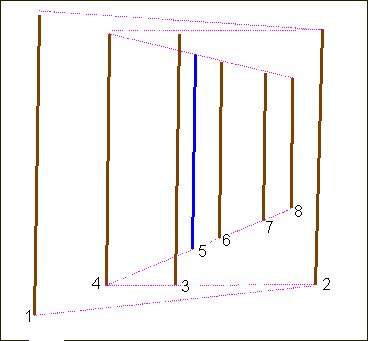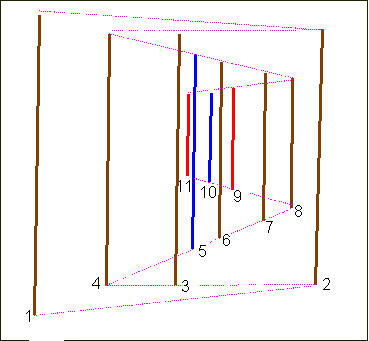
We already said that the coloured bars are depicted according to very rigorous prospective rules. Jurg Spiller
[11] already suggested a possible reading of the perspective, as showed in Animation 4, where the bars, from 1 to 11, are connected by ideal zigzagging pathways both at the bottom and at the top.Animation 4
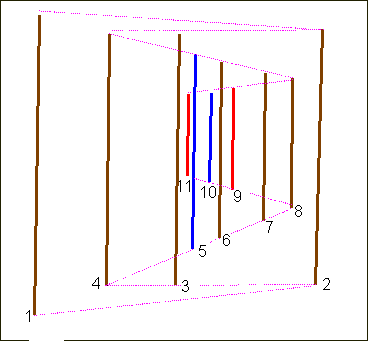
In order to stress the careful perspective, notice that the bars form several perspective planes (with reference to Sketch 3 they are: 1-2, 2-4, 4-8, 8-11), whose vanishing points are aligned along the same horizon line. This line divides the checkerboard in two parts whose highs are respectively 5 cells and 3 cells.
Sketch 3
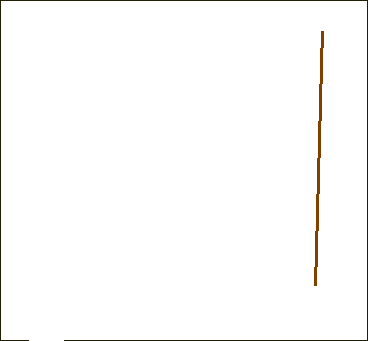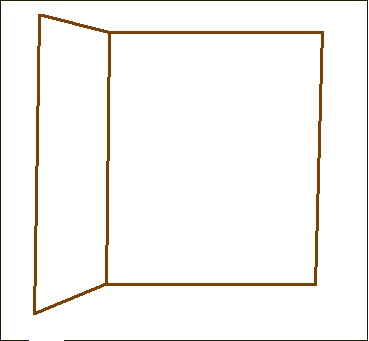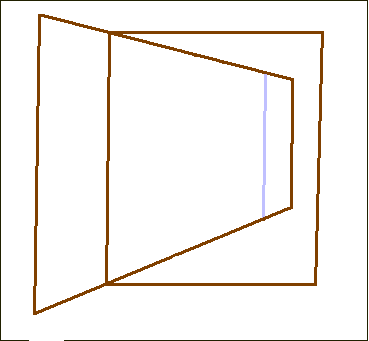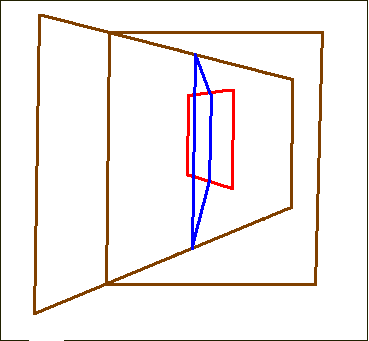
However other interesting readings are also possible. As for me, I prefer the one displayed in Animation 5.
Animation 5
Of course it maintains the important property of the alignment of the vanishing points of the perspective planes along the same horizon as in Spiller’s proposal; see the following Sketch 4:
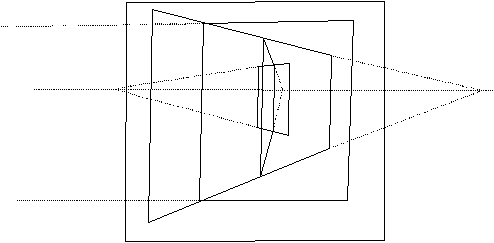
Sketch 4
There are several reasons for my preference.
First, it is consistent with the use of the different colours, because each perspective plane is made by bars of the same colour, while the planes in Sketch 3 contain bars of different colours (the plane containing bars from 4 to 8 contains brown and blue colours, while the plane from 8 to 11 contains brown, red and blue bars).
Second, this alternative reading avoids breaking the alignments of the bars, as instead happens in Sketch 3, where bar 1 is in fact aligned with the ones from 4 to 8, but the pathway chosen by Spiller breaks this continuity.
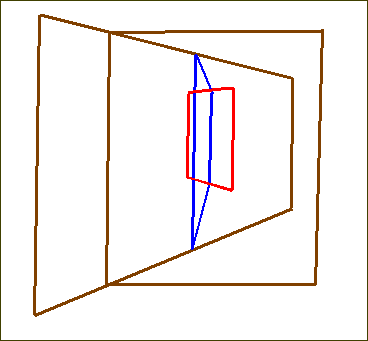
Third (see Sketch 5) the planes have with each other those typical T-junctions (even though not necessarily right-angled) that Klee often used, and this suggests (at least indirectly) something iterative (a plane T-joined with another, which is T-joined with another, and so on).
Sketch 5
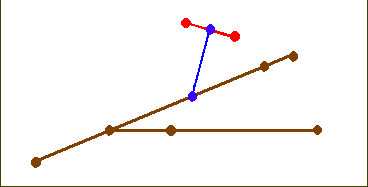
Fourth, the pathway described by the planes recalls a branching process (shown in Sketch 6, where the planes of Sketch 5 are sectioned by a transversal plane; the nodes in Sketch 6 mark the position of the bars).
Sketch 6
It is well-known that Klee was deeply involved by growth processes in Nature, especially those of the plants; sketches of vegetable elements similar to the one in Sketch 6 are very frequent in his paintings and drawings, throughout his whole artistic career. The interesting thing is that each branch in Sketch 5 shows a number of nodes corresponding to a Fibonacci’s number (Fibonacci’s numbers are: 1, 1, 2, 3, 5, 8…); in addition, recall that the horizon line divides the checkerboard in two parts whose highs are in the ratio 5:3 which in turn sums to 8, all of them being Fibonacci’s numbers. In fact Klee knew Fibonacci’s series and its relation to the golden section
[12]. Thus the possible use of the numeric progression is a new suggestion of something iterative. Furthermore recall that Fibonacci’s numbers govern the phyllotaxis (leaf arrangement in the plants); at that time, several accounts on phyllotaxis and Fibonacci’s numbers were available; D’Arcy Thompson summarised them in the fourteenth chapter of his masterwork [13].
Finally, Sketch 7 emphasises that the segments in Sketch 6 seem to suggest something like a spiralling motion, enveloped by the segments, similar to those generated by L-systems
[14].Sketch 7
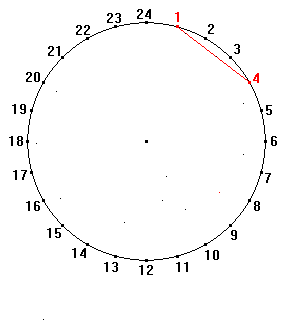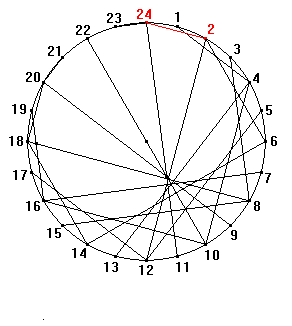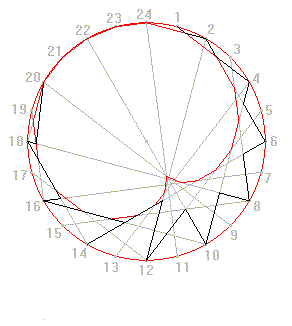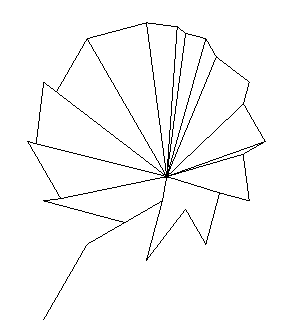
Iterative procedures generating tangent envelopes were explicitly used by Klee in the cited progressions inside the circle, as in the famous drawing The truth about the palm-leaf (see Animation 6, based on the analysis made by Klee himself
[15]).Animation 6
Let us resume now the elements characterising the bar system useful for my further argumentation: the system undergoes a perfect perspective construction. I have been proposing a perspective reading based on dynamic iterative growth processes that imply a spatiality characterised by rotatory motion and T-junction.