1.2. Deterministic chaos
So far I presented the three major key ingredients in Klee’s thought useful for my argumentation: presence of chaos in Nature, primacy of formation on form, use of iteration as a constructive tool.
Now, let us briefly recall the concept of deterministic chaos in dynamic systems, to compare it later with Klee’s results. The most popular way to do that, is to present the unexpected behaviour of the simplest example of non-linear dynamic system: the discrete-time version of the so called logistic model. It is the following difference equation:![]() , which iteratively takes the input
, which iteratively takes the input ![]() to calculate the next value
to calculate the next value![]() .
.
The equation was at first introduced to model the growth of biological populations, because of its typical asymptotic behaviour, corresponding to the progressive reduction of the growth rate of the same population, as it gets closer to the capacity of the environment (expressed in terms of density of population sustainable by that environment).
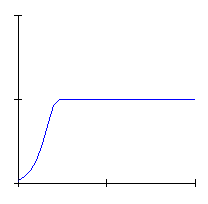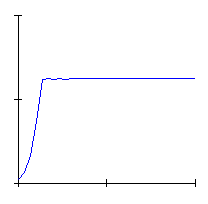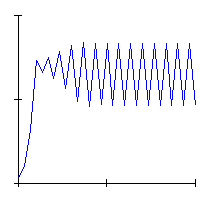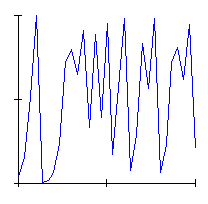
We know that such a model shows several qualitatively different behaviours, as the value of the parameter ![]() increases. Look at Animation 1, which displays the variation of population density in time: indeed the typical sigmoid shape soon changes its own aspect, showing at first an oscillating motion above and below with periodicity 2, which progressively becomes ever more complicated, with a typical doubling cascade of the period, and finally the movement become absolutely unpredictable and chaotic
increases. Look at Animation 1, which displays the variation of population density in time: indeed the typical sigmoid shape soon changes its own aspect, showing at first an oscillating motion above and below with periodicity 2, which progressively becomes ever more complicated, with a typical doubling cascade of the period, and finally the movement become absolutely unpredictable and chaotic
Animation 1
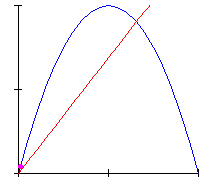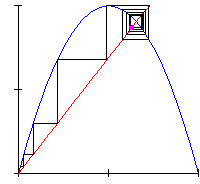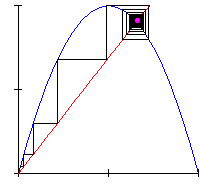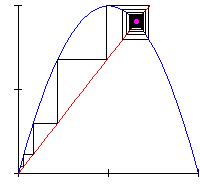
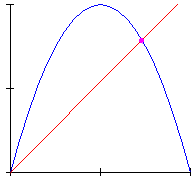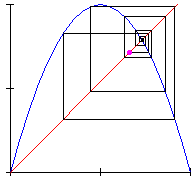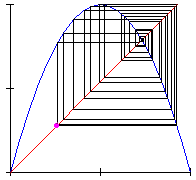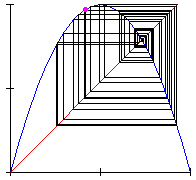
The same dynamics is also often displayed by means of cob-web diagrams like that in Animation 2, which maps the density at the time n versus the density at the time n+1: here we see the system gradually converging toward its stable steady state, at the intersection of the straight line with the parabola, corresponding to the asymptotic behaviour.
Animation 2
Look finally at Animation 3: for convenient values of the parameter ![]() we have a completely different dynamic behaviour of the system, which is chaotic.
we have a completely different dynamic behaviour of the system, which is chaotic.
Animation 3
I reminded the use of the cob-web diagrams for two reasons: first, they are useful to better understand the iterative and deterministic character of the model, and second, they help us understand the deep meaning of Klee’s procedures I will present in a successive sections of the paper.